COMS 4995 Advanced Systems Programming
Caching, Memory Mapping, and Advanced Allocators
Memory Hierarchy
The pyramid shown below (CSAPP Figure 6.21) depicts the memory hierarchy in computer systems:
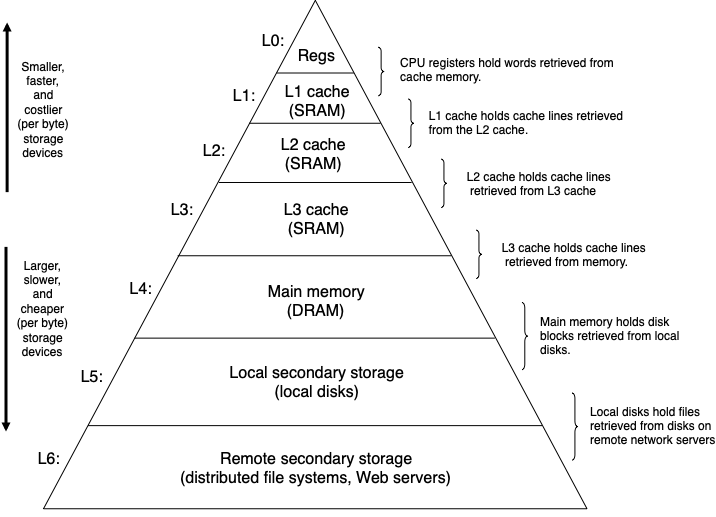
The triangular shape refers to the size, speed, and cost of the storage devices. Devices at the top are smaller, faster, and costlier than the devices towards the bottom of the pyramid. Each level of the pyramid serves as a cache for the level underneath.
- Registers: small number of fast storage units embedded in CPUs
- Intel Core i7 has 16 64-bit general purpose registers
- No added access latency
- Cache: small amount of memory between registers and RAM
- Uses SRAM, which is faster and more expensive than DRAM
- Several levels of cache to bridge growing disparity between CPU and RAM in speed and capacity
- Intel Core i7 has 64KB of L1, 256KB of L2, and 8MB of L3
- Latencies: 4 cycles for L1, 10 cycles for L2, 50 cycles for L3
- Usually accessed in 64-byte blocks called “cache lines”
- Main memory: volatile storage for code and data for running programs
- Typical laptops have 4GB to 32GB of DRAM
- Latency: 200 cycles
- Usually accessed in 4KB chunks called “pages”
- Local storage: persistent storage for program and data files
- Typical laptops have 256GB to 4TB SSDs
- Typical desktops have 512GB to 8TB HDDs
- Latency: 100,000 cycles for SSD, 10,000,000 cycles for HDD
Cache-conscious Programming
Principle of Locality
-
Temporal locality: Once a memory location has been referenced it is likely to be referenced again in the near future
-
Spatial locality: Once a memory location has been referenced, nearby memory locations are likely to be referenced in the near future
2-dimensional Arrays in C
Let’s motivate our study of cache-conscious programming by working with 2-dimensional arrays in C.
Consider the following 2-dimensional array declaration in C:
int a[3][2];
The array is laid out in row-major order in memory as follows:
+---------+---------+---------+---------+---------+---------+
| a[0][0] | a[0][1] | a[1][0] | a[1][1] | a[2][0] | a[2][1] |
+---------+---------+---------+---------+---------+---------+
Example 1: Summing Matrix Elements
Consider the following nested loop that computes the sum of all elements in a M x N matrix a:
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
sum += a[i][j];
}
}
This algorithm exhibts good spatial locality. We are accessing the elements of
a one-by-one as they are laid out in memory, i.e., stride-1 reference pattern.
Each cache miss will be handled by bringing in a cache-line sized chunk of a,
which will result in subsequent cache hits for the rest of the elements residing
in the cache-line.
There is also good temporal locality in the loop body. The local variables
sum, a, i, and j are referenced each time in the loop body. An
optimizing compiler will probably cache these variables in registers.
On the other hand, the following modified version of the nested loop exhibits poor spatial locality:
for (int j = 0; j < N; j++) {
for (int i = 0; i < M; i++) {
sum += a[i][j];
}
}
Here, the order of the loops have been switched. We are now accessing the matrix column-by-column instead of row-by-row, which is not the order in which the elements are laid out in memory. Unless the entire matrix can fit in the cache, this reference pattern will result in significantly more cache misses than the previous version.
Example 2: Matrix Multiplication
Let’s continue to study the effect of rearranging nested loops on cache
performance by considering various matrix multiplication implementations from
CSAPP Figure 6.44. The following three code snippets (Figures 6.44 a, d, and f)
multiply two N x N matrixes a and b, yielding matrix c. We focus our
analysis on the inner-most nested loop.
First consider code snippet 1:
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
sum = 0;
for (int k = 0; k < N; k++) {
sum += a[i][k] * b[k][j];
}
c[i][j] += sum;
}
}
- There are two memory loads and zero memory stores. We do not count loading
from and storing into the local variable
sumbecause we assume that the compiler will cache sum into a register. This is why the code usessumin the inner loop instead of repeatedly accessingc[i][j]. ais accessed in stride-1bis accessed in stride-N
Next consider code snippet 2:
for (int k = 0; k < N; k++) {
for (int j = 0; j < N; j++) {
r = b[k][j];
for (int i = 0; i < N; i++) {
c[i][j] += a[i][k] * r;
}
}
}
- There are two memory loads and one memory store
aandcare both accessed in stride-N
Finally consider code snippet 3:
for (int i = 0; i < N; i++) {
for (int k = 0; k < N; k++) {
r = a[i][k];
for (int j = 0; j < N; j++) {
c[i][j] += r * b[k][j];
}
}
}
- There are two memory loads and one memory store
bandcare both accessed in stride-1
Benchmarking these three snippets with large enough size N reveals that
snippet 3 runs the fastest, followed by snippet 1, and snippet 2 performs the
worst. The runtimes are largely determined by the snippets’ cache performances.
Snippet 3 performs the best by far due to its stride-1 reference pattern for
both b and c. Snippet 1 performs worse than snippet 3 due to its stride-N
access on matrix b despite having fewer memory accesses. Snippet 2 performs
worst by far due to its stride-N access to both matrices.
Summary
- Optimize the inner loops of your program, which tends to dominate computation and memory access
- Strive for stride-1 reference pattern to maximize spatial locality in your program
- Once data has been read from memory, try to use it as much as possible to maximize temporal locality in your program
Memory Mapping using mmap()
Instead of performing I/O with read()/write() we can map a region of the
file into the address space and treat it like an array of bytes. The kernel
ensures that updates to this region of memory will get written to the
corresponding region on disk. This mapping can be viewed as an example of using
main memory as a cache for disk. This is demonstrated by APUE Figure 14.26:
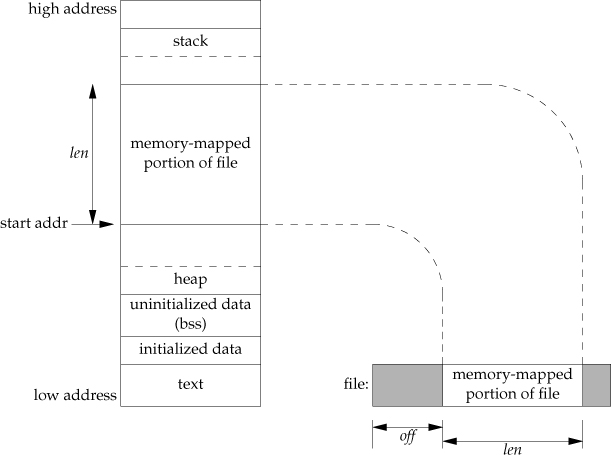
Recall that the virtual address space is broken up into pages (typically 4KB) and that the OS kernel maintains a mapping from these virtual pages to physical pages in RAM:
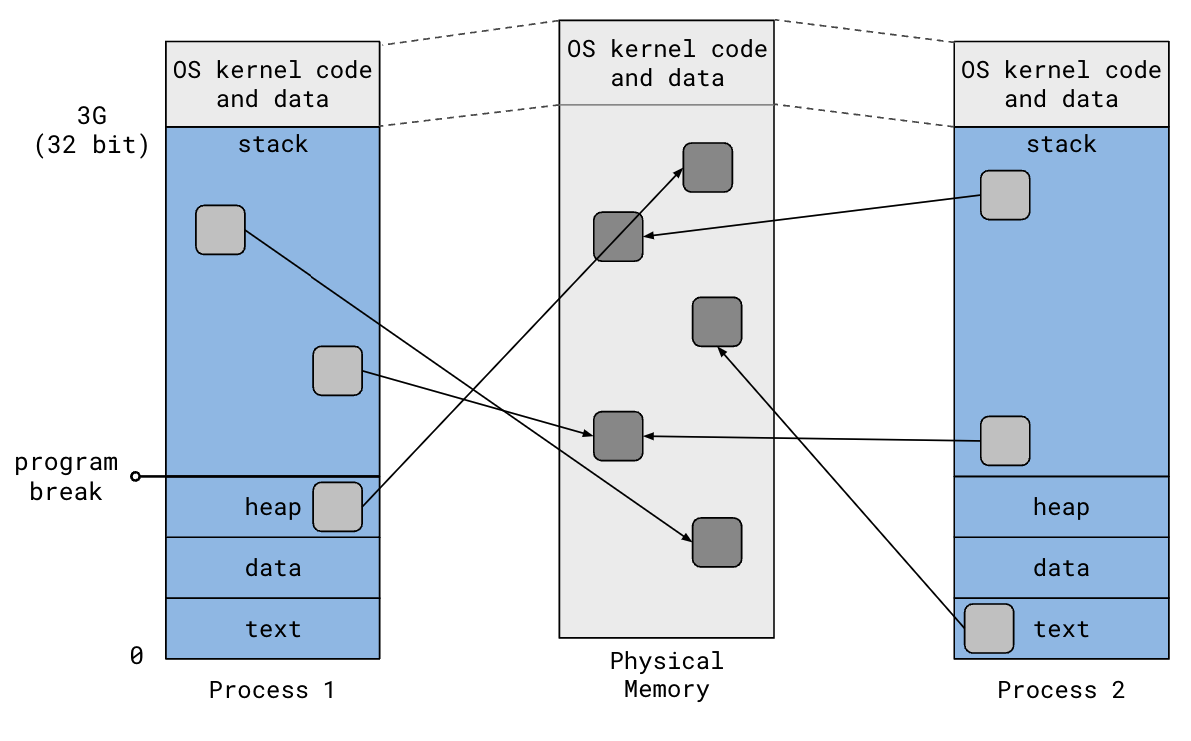
File-backed mappings add an additional mapping from physical pages in RAM to regions of disk. Two processes can map the same region of a file into their address space and see each other’s updates to the file. The OS kernel maps the virtual pages of the two processes to the same physical pages, so updates made by one process is immediately reflected in the other process even before the contents get written to disk. In fact, if you just want two processes to share the same memory, you can remove the file from the equation and create an anonymous memory mapping.
The mmap() system call creates new memory mappings:
#include <sys/mman.h>
void *mmap(void *addr, size_t length, int prot, int flag, int fd, off_t offset);
// Returns: starting address of mapped region if OK, MAP_FAILED on error
Here is a brief explanation of the parameters:
- addr: The suggested starting address of the new mapping. Prefer to pass
NULLand letmmap()decide the starting address and return it - length & offset: The length and offset of the mapping
- prot: Protection of the mapped region (e.g., read, write, execute)
- flag: Visibility and other modifiers
MAP_SHARED: Updates to the mapping are visible to other processes, and are carried through to the underlying fileMAP_PRIVATE: Updates to the mapping are not visible to other processes, and are not carried through to the underlying fileMAP_ANONYMOUS: The mapping is not backed by any file. This has the effect of simply allocating memory to the process when used withMAP_PRIVATE
- fd: File descriptor for the file to be mapped. Use -1 for anonymous mapping
Advanced Allocator Strategies
Having discussed memory hierarchy, cache-conscious programming, and memory mappings, we can now complete our discussion of allocators.
Explicit Free List
Recall the optimization from last lecture: repurpose the unused payload in free blocks for two pointers to link together free blocks explicitly:

With the explicit free list, searching for a free block only requires iterating through free blocks in the list, as opposed to all blocks, which was the case was with the implicit free list.
The explicit free list needs to be updated whenever a block is freed. Where should the newly freed block be placed?
An obvious strategy is to maintain the free list in LIFO order: simply insert the newly freed block at the beginning of the list. The following diagram illustrates this:
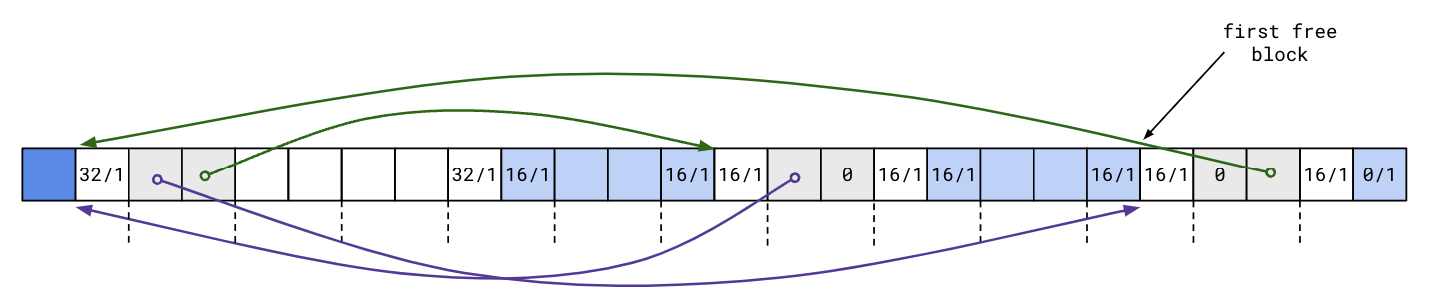
This approach is simple and fast, and may benefit from temporal locality. Reusing a recently freed block means that its memory location may still be in the cache and we don’t have to use a new cache line, possibly evicting other data from the cache.
Segregated Free Lists
We can further optimize free list search time and memory usage by maintaining multiple free lists. Each free list contains blocks of the same or similar size.
For example, we can partition the block sizes by powers of 2:
- Bucket 0: 32-63 bytes
- Bucket 1: 64-127 bytes
- Bucket 2: 128-255 bytes
- Bucket 3: 256-511 bytes
- Bucket 4: 512-1023 bytes
- Bucket 5: 1024-2047 bytes
- Bucket 6: 2048-4095 bytes
- Bucket 7: 4096+ bytes
Real Life Allocators
GNU libc Implementation
- Reduce contention in multi-threaded environments
- Shard heap into multiple separate “arenas”
- Per-thread caching of recently freed blocks
- Handle huge requests off the heap by asking the OS kernel directly using the
mmap()syscall, which creates new page mappings for the process - Deferred coalescing: maintain fast turnaround free lists to keep around recently freed blocks that haven’t been coalesced yet
- Segregated storage: maintain small bins holding fixed-size chunks and large bins holding ranges of chunk sizes
- Periodically shrink the heap when memory blocks at the top of the heap are freed
References:
- https://azeria-labs.com/heap-exploitation-part-2-glibc-heap-free-bins/
- https://sourceware.org/glibc/wiki/MallocInternals
Industry Implementations
TCmalloc, from Google, and jemalloc, from FreeBSD and currently maintained
by Facebook, are some alternatives to GNU libc’s implementation. These
allocators are optimized for highly concurrent workloads. We’ll revisit some of
the techniques used by these allocators when we cover threads later in the
course.
Memory Pool Allocator
A program may rely heavily on frequent allocations and deallocation of the same kind of object (e.g., graph algorithm managing fixed-size node objects). Instead of using a general purpose allocator, such programs can use a specialized memory pool allocator for that object.
The pool allocator will allocate a large region of memory (e.g., some multiple of page size), and divide it into equal sized objects. Allocation and deallocation are as simple as marking an object used and freed, respectively. The fixed-size chunks eliminates external fragementation seen in general-purpose allocators due to their support for variable-sized chunks.
Last Updated: 2024-01-29