COMS 4995 Advanced Systems Programming

Introduction to Memory Allocators

Process Memory Address Space

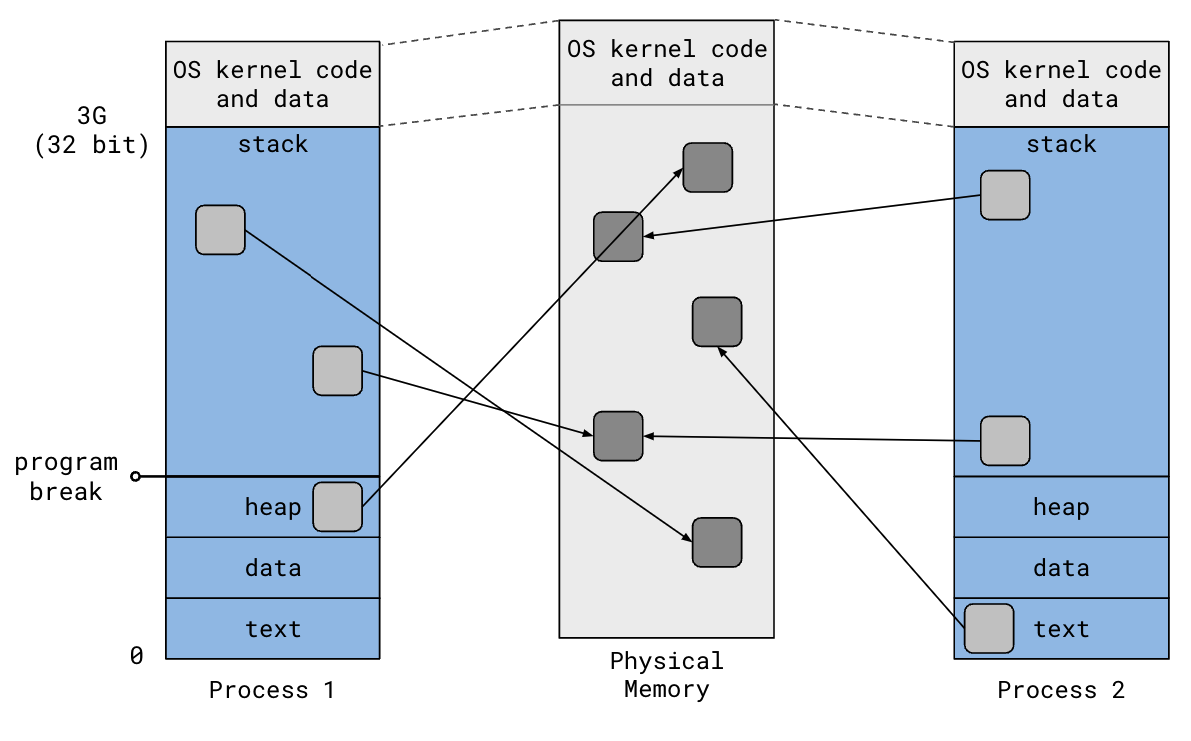
Recall the 32-bit virtual address space of a process:

• Text: program code
• Data: static variables
• Heap: dynamically allocated memory, grows upward
• Stack: automatic memory, grows downward
• OS kernel code & data, shared by all processes

The term “program break” refers to the top of the heap. Increasing the program break has the effect of allocating memory; decreasing the break deallocates memory. The brk() system call is used to change the program break.

The diagram shows that the virtual address space is broken up into chunks called “pages” (typically 4KB). The OS kernel maintains a mapping from virtual pages to physical pages. When a program accesses memory, the CPU translates the virtual address to the corresponding physical address. This enables multiple process to have independent virtual address spaces backed by the same physical memory.

Programs could certainly use the heap as a single contiguous memory region, using the brk() system call to grow and shrink it as needed. But most programs tend to create and destroy many arbitrarily-sized objects during execution. Having user programs manually manage memory only using brk() is tedious and difficult to get right, leading to wasteful memory usage. Instead, most programs use a memory allocator, which provides a simple API to allocate and release memory blocks on the heap. The C standard library provides a general-purpose memory allocator implementation through malloc() and free().

malloc() and free()

The following diagram (Figure 9.34 from CSAPP) illustrates how malloc() and free() manage the heap:

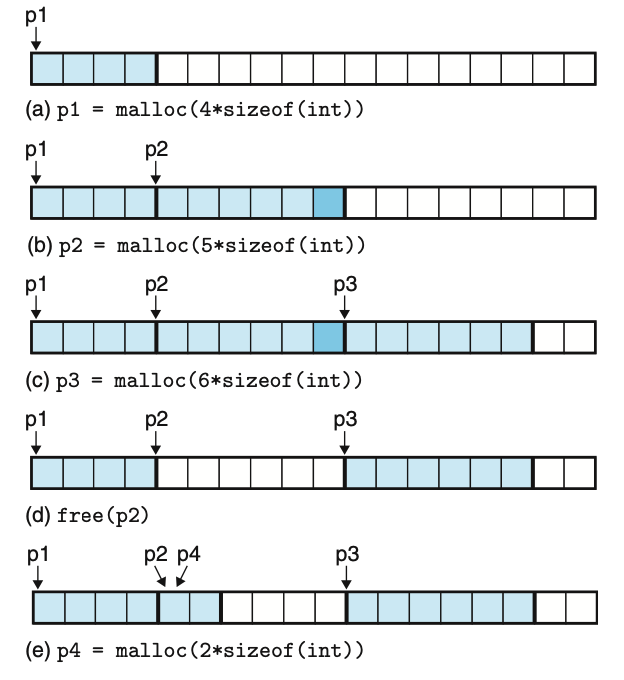
Each block represents 4 bytes of memory. As expected, (a) allocates 16 bytes. But (b) allocates 24 bytes instead of the expected 20 bytes. The extra 4 bytes of “padding” are there to ensure the next allocated block will be aligned at an 8-byte boundary. All memory blocks returned by malloc() are required to start at an address that is a multiple of 8 on 32-bit systems or 16 on 64-bit systems. This is to ensure efficient memory access by the hardware. The padding bytes is an example of internal fragmentation, which refers to the waste when more memory had to be allocated than was requested.

(d) releases the 24 bytes previously allocated in (b), making it available for a future allocations. In (e), the allocator has two options to satisfy the 8-byte request: either it can use the 8 bytes at the end of the heap or it can take 8 of the 24 bytes freed in (d). The diagram shows the second option.

This example illustrates how the underlying selection algorithm affects memory utilization. If the allocator had chosen the 8 bytes at the end of the heap, there would have been 24 bytes available in one contiguous region. However, since it chose to allocate in the region freed by (d), the 24 bytes left available are not in one contiguous region. A future call to malloc(24) would succeed under the first strategy, but fail under the second. This is an example of external fragmentation, where memory is spread out into smaller pieces, making the allocator unable to satisfy larger requests.

Implicit Free List

Now that we’ve seen how malloc() and free() work at a high level, it should be clear that they must be maintaining metadata to be able to answer the following questions:

• Which regions of the heap have been allocated and which are free?
• Given only a void * passed to free(), how many bytes should be released?

Block Structure

The following diagram (Figure 9.35 from CSAPP) proposes a simple heap block structure for 32-bit systems that addresses these questions:

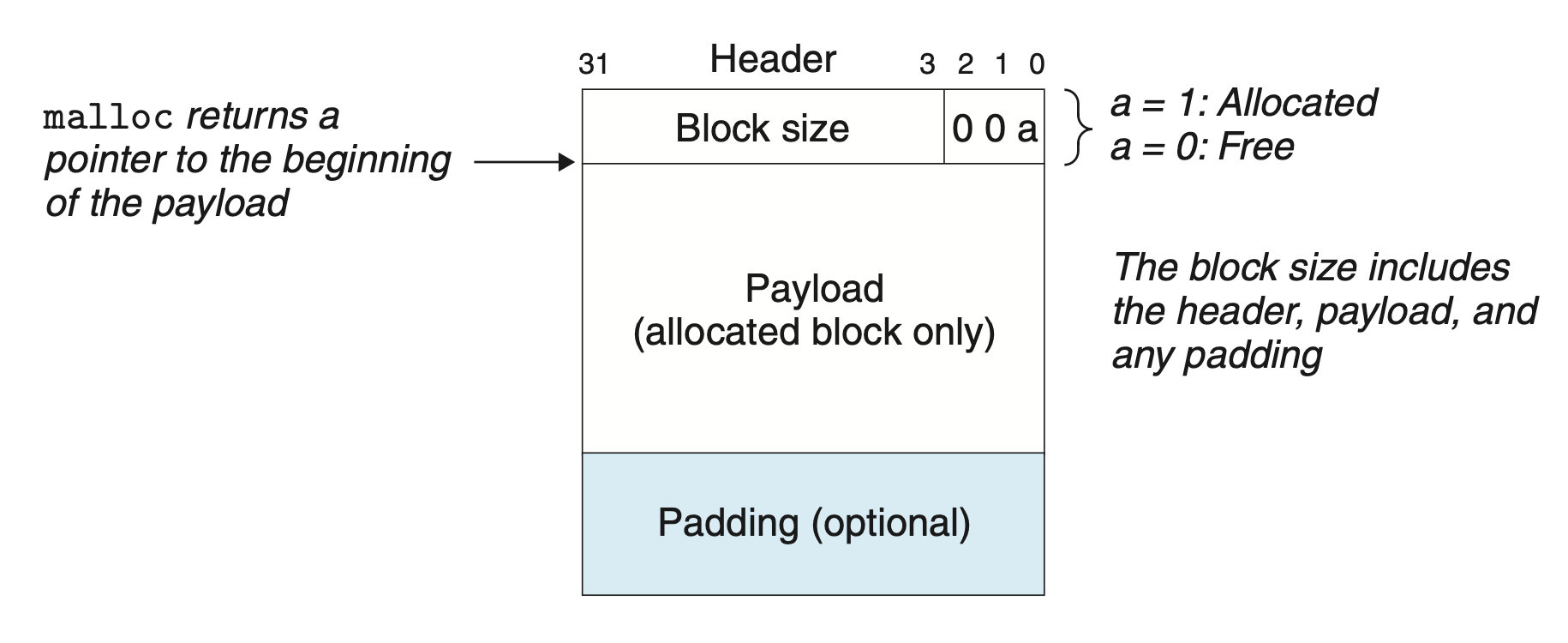
There is a 4-byte header right before the user payload to store the block size and a bit to indicate whether or not the block has been allocated. Since block size is always a multiple of 8 (we’ll revisit this detail in the next diagram), the lower 3 bits are unused. Repurpose one of them as the allocated bit.

Figure 9.36 from CSAPP shows how the heap can be organized using this block structure:

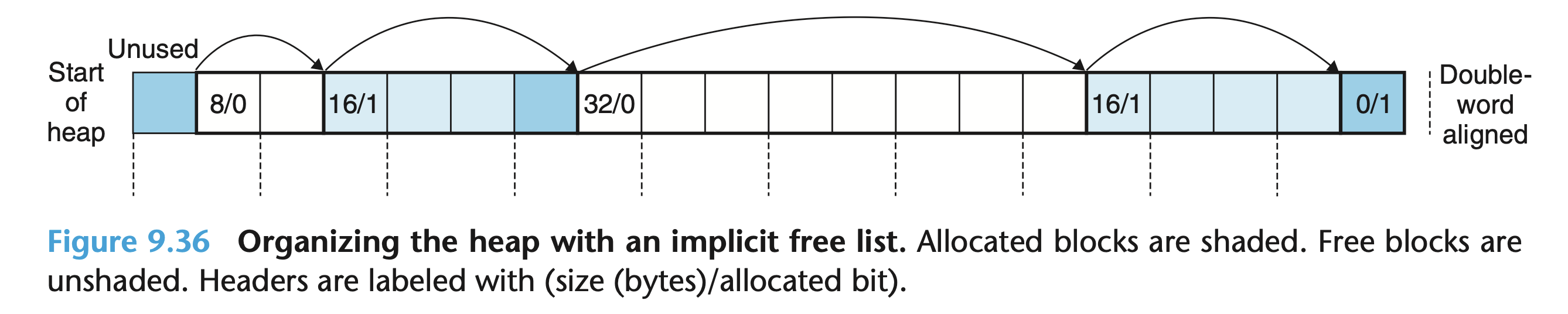
Recall that all user payloads must start an 8-byte boundary in 32-bit systems. The diagram indicates these boundaries with dotted lines. Take for example the 16-byte allocated block towards the beginning of the heap. This block was allocated as a result of a call to malloc(8). To ensure that the next block’s payload starts at an 8-byte boundary, a 4-byte padding was added to end, making the total block size 16 bytes including the header. A block’s header, payload, and possible padding will always make the block’s size a multiple of 8.

There are 4 bytes of padding at the beginning of the heap to ensure the first block’s payload is at an 8-byte boundary. There is a special “epilogue” block at the end of the heap with size 0, which the textbook’s implementation uses as a terminator.

Below is psuedocode demonstrating how we can use this block structure to implement malloc():

char *heap_start = NULL;

// __init_heap() would be called before main() to initialize the heap
void __init_heap() {
    // Get the initial program break and grow heap by arbitrary amount, e.g., 4KB
    heap_start = sbrk(4096);
    // Skip the leading 4-byte padding
    heap_start += 4;

    // Initalize implicit free list, etc.
    // ...
}

void *malloc(size_t size) {
    // Adjust size to include header and satisfy alignment requirements, etc.
    // ...

    // Loop through all heap blocks
    char *block = heap_start;
    while (1) {
        uint32_t header = *(uint32_t *)block;
        // Extract block size and allocated bit from the packed header
        size_t block_size = header & ~0x7;
        int allocated = header & 0x1;

        // This is the epilogue block -- we've reached the end of the heap
        if (block_size == 0)
            return NULL;

        // First fit strategy: return the first block big enough for the
        // request. Next fit and best fit are alternative strategies, but
        // require more work
        if (!allocated && size <= block_size) {
            // Update the block's header to set the allocated bit
            *(uint32_t *)block = block_size | 0x1;

            // Note that we claimed the entire block regardless of how big it
            // actually was. We could have turned the excess bytes into a new
            // free block by initializing a new header after this block.

            // Return a pointer to the payload
            return block + 4;
        }

        // Iterate to the next block
        block += block_size;
    }
}

Coalescing Free Blocks

Consider CSAPP Figure 9.38:

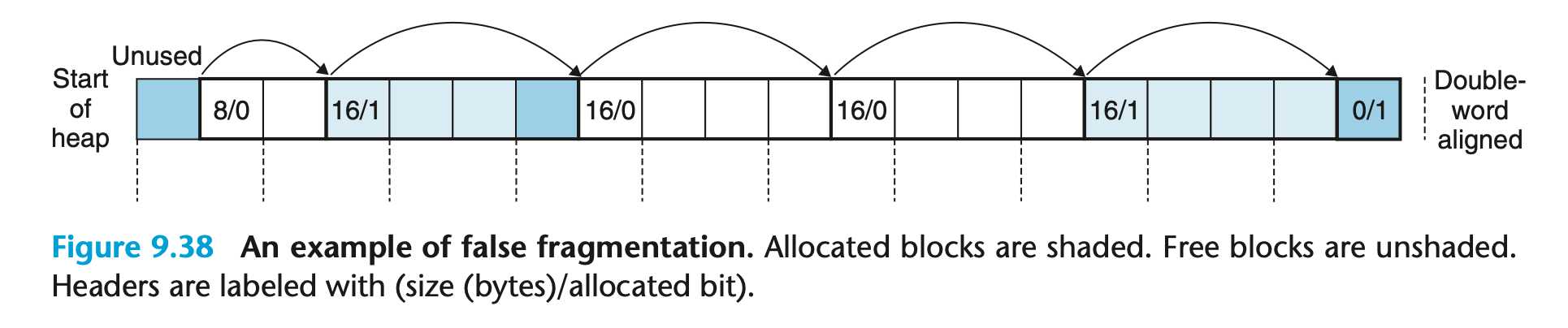
Note that there are two 16-byte free blocks next to each other in the middle of the heap after some sequence of malloc() and free() calls. A call to malloc(20) would fail even though there is clearly more than enough space available. This is known as false fragmentation. If the two 16-byte free blocks had been merged, we could have served that allocation request.

When free() is called, the allocator can attempt to coalesce the given block with its neighbors, if they are free, creating one larger block with an updated block size. The next neighbor can be reached simply by advancing the given pointer by the given block’s size. But how do you reach the given block’s previous neighbor?

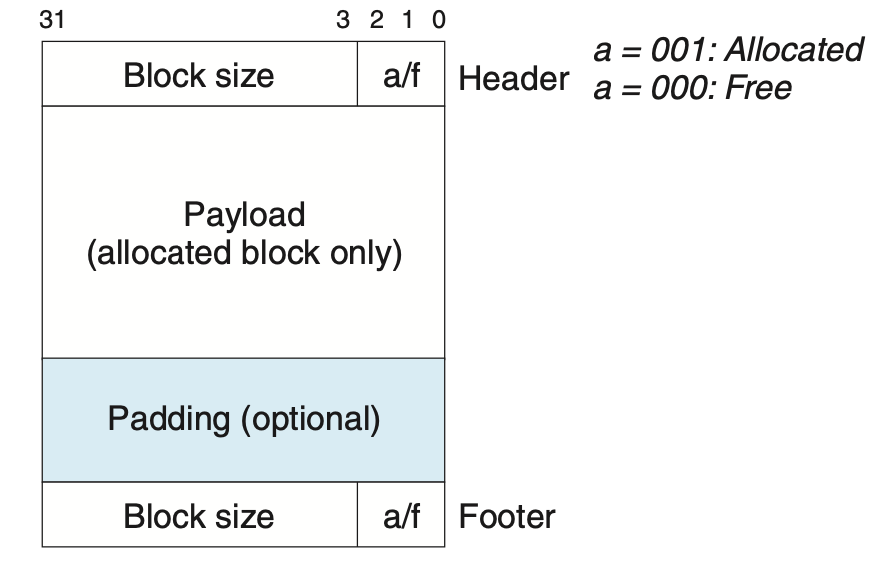
One solution is to duplicate a block’s header at the end of the block. This footer, or “boundary tag”, enables us to traverse backwards in the free list because a given block’s header is right after the previous block’s footer, which contains the previous block’s size. This is depicted in CSAPP Figure 9.39:

From Implicit to Explicit

The implicit free list we’ve been discussing uses the block size as a “pointer” to the next/previous block in the list. This means that searching for a free block in the list requires going through all blocks in the list, which also includes the allocated blocks. One can imagine constructing an explicit free that only links together free blocks.

We can take advantage of the fact that a free block’s payload is unused by repurposing it to store explicit pointers to the prev/next free blocks, as demonstrated in CSAPP Figure 9.48:

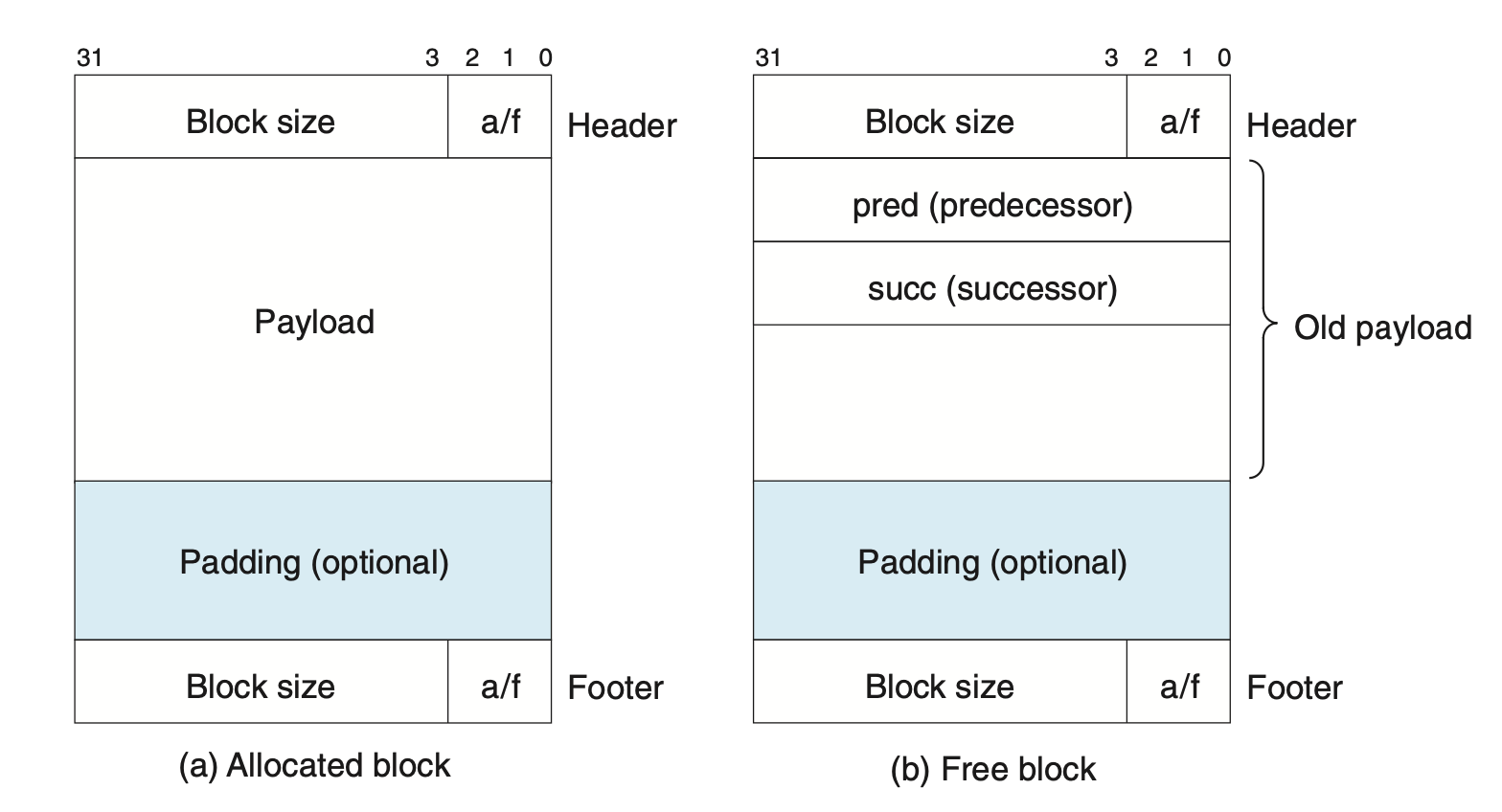
Given the block structure we’ve built up so far, where each block has a 4-byte header and a 4-byte footer, the payload will always be at least 8 bytes to satisfy the alignment requirement on 32-bit systems. Therefore, free blocks can always hold two 4-byte pointers without increasing the minimum block size.

We’ll revisit explicit free list management next time!

---

Last updated: 2024-01-12